Trabalho – Computação Grafica
- Sistema de Visão Humana
O sistema de visão humana é responsável por reconhecer, identificar e analisar tudo o que está a sua frente. O olho humano é órgão sensorial complexo que captura relações espaciais e temporais de objetos e converte energia luminosa em sinais elétricos para serem processados pelo cérebro. Até chegar ao cérebro esta energia luminosa percorre um trajeto, onde se inicia na córnea, onde ocorre a entrada do sinal luminoso; a retina converte este sinal luminoso em sinal elétrico que são transmitidos ao cérebro através do nervo óptico. Na retina existem cerca de 100 milhões de sensores, responsáveis por converter os estímulos luminosos para os sinais elétricos que serão processados pelo cérebro. Enquanto os seres humanos possuem 100 milhões de sensores as câmeras atuais possuem 16 milhões, por isso não é possível comparar a qualidade de uma imagem de câmera com a visão humana.
O sistema visual não é simplesmente uma câmera, é um receptor e um registrador de informações, onde os olhos junto com o cérebro constituem num sistema de informações que analisa e processa tudo o que está no mundo. O olho é o receptor de energia luminosa e o cérebro dedica bilhões de seus neurônios e trilhões de suas sinapses à visão.
O cérebro possui dois hemisférios, o direito e o esquerdo, e cada um controla um campo de visão, sendo que o hemisfério direito controla o campo de visão da esquerda e o hemisfério esquerdo controla o campo de visão da direita. Segue abaixo uma imagem do olho humano.

Observando o olho é possível caracterizar cada uma de suas partes e definir suas funções individualmente, sendo estas as seguintes:
- Esclerótica: Membrana elástica, parte branca do olho.
- Córnea: Parte responsável pela captura de luz.
- Íris: Membrana colorida com um orifício negro no centro.
- Cristalino: Responsável pelo foco.
- Humor vítero: Substância gelatinosa que está localizada atrás do cristalino.
- Humor aquoso: Câmara preenchida com um fluido, localizada atrás da córnea.
- Pupila: Orifício para passagem de luz.
- Retina: Conversor de sinais de luz em sinais elétricos.
- Nervo ótico: Transmite sinais para o cérebro.
O olho humano enxerga os objetos de ponta cabeça e invertidos, e o uma passagem de 17 mm que transforma o objeto na posição real.
- Diferenças entre o modelo RGB e CMYK
Os dois sistemas de modelos de cores existentes são o RGB e o CMYK. O RGB representa as cores vermelha (Red), verde (Green) e azul (Blue) e a junção destas cores chega à cor branca. Já o sistema CMYK trabalha com as cores ciano (Cyan), majenta (Majenta), amarelo (Yellow) e preto (Key), onde a mistura delas chegam a cor preta.

| RGB | CMYK | |
| Junção das cores | Resulta no branco | Resulta no preto |
| Qualidade | Menor | Maior |
| Reprodução | Em TV, monitores e computadores | Em imprensas, impressoras e fotocopiadora. |
| Funcionamento | Cores básicas perceptíveis | Através da absorção de luz |
| Base | Triângulo tricromático de Maxwell | Sistema de quadricromia
|
- Sistema de Coordenadas
O Sistema de Coordenadas e representado por eixos e pontos, partindo da premissa que existem alguns tipos de Sistemas de Coordenados, serão apresentados os que são voltados para a área de computação.
Podem ser utilizados diferentes sistemas de coordenadas para descrever os objetos em um sistema 2D. Ele é utilizado para dar uma referência em termos de medidas, tamanho e posição.
Um determinado sistema de coordenadas é denominado Sistema de Referência, e se dividi quatro tipos, Sistema de Referência do Universo (SRU), Sistema de Referência do Objeto (SRO), Sistema de Referência Normalizado (SRN) e Sistema de Referência de Dispositivo (SRD).
- Sistema de Coordenadas do Plano Cartesiano
O plano cartesiano é representado a partir de um sistema de eixos ortogonais que possui duas retas orientadas e perpendiculares entre si, o eixo x, chamado de eixo das abscissas e o eixo y, chamado de eixo das ordenadas. Segue abaixo a representação destes eixos.

Figura 1.1 – Plano Cartesiano
A partir deste plano é possível indicar pontos, e a junção de dois pontos forma uma reta, por exemplo, um ponto P recebe valores para x e para y, na seguinte forma: P = (x,y).
Exemplo: P = (4,3)

Figura 1.2 – Ponto P = (4,3)
Partindo deste princípio, é possível colocar infinitos pontos dentro de um plano cartesiano. Este modelo, que utiliza os eixos x e y, é conhecido com plano 2D, ou bidimensional, há também o plano 3D, onde a característica acrescentada é a existência de um eixo z q possibilita a criação de objetos tridimensionais.
 Figura 1.3 – Eixos x, y, z
Figura 1.3 – Eixos x, y, z
O próximo tipo de sistema de coordenadas é o Sistema de Coordenadas Polares.
- Sistema de Coordenadas Polares
O Sistema de Coordenadas Polares é baseado na medida do ângulo em relação a um ponto fixo e um semi-eixo fixo. Onde o ponto fixo é chamado de origem e o semi-eixo fixo de reta polar.
 Figura 1.4 – Ponto fixo (O), semi-eixo fixo (x) e ângulo (θ)
Figura 1.4 – Ponto fixo (O), semi-eixo fixo (x) e ângulo (θ)
O gráfico para representação dos pontos possui os mesmo eixos do plano cartesiano, e eixo das abscissas e das ordenadas, a figura abaixo mostra os ângulos e os quadrantes do gráfico, onde quando o cálculo se torna negativo é feita a amostragem no sentido anti-horário, como indica a figura abaixo.
 Figura 1.5 – Gráfico sistema de coordenadas polares
Figura 1.5 – Gráfico sistema de coordenadas polares
- Coordenadas Homogêneas
De acordo com a definição do site Professor Global (professorglobal.cbpf.br) Coordenadas Homogêneas ou coordenadas de projeção é a representação de um ponto com coordenadas cartesianas (x,y) como (x’, y’, t) onde x’ = tx e y’ = ty. Para um dado plano isso é equivalente a escolher um ponto fora do plano e representar qualquer ponto neste plano pela linha que une ao ponto de referência.
As coordenadas homogêneas utilizam operações matriciais que diferem entre adição, para movimento de translação, e multiplicação para o escalonamento e rotação. Os cálculos que são utilizados são os seguintes:
- P’ = P + T
- P’ = R . P
- P’ = S . P
Para tratar as transformações através de uma mesma operação são utilizadas as coordenadas homogêneas, onde todas as transformações são tratadas através de multiplicação, portanto, o cálculo fica da seguinte maneira:
- P’ = (R ou S ou T) . P
As transcrições são escritas da seguinte maneira:

- Transformações Geométricas
As principais transformações são a de Rotação, Translação e Escalonamento. Cada uma delas será explicada separadamente juntamente com o exercício proposto pelo ATPS.
- Escalonamento
O escalonamento é a mudança de tamanho da figura, projetando-a em uma escala maior ou menor, de acordo com a necessidade, sendo que a mesma tem um ponto inicial para que o escalonamento seja feito. A figura a seguir irá mostrar como ocorre e qual a fórmula matemática utilizada para realizar o cálculo.
 Figura 3.1 – Exercício 1 – Escalonamento
Figura 3.1 – Exercício 1 – Escalonamento
- Nome da Transformação: Escalonamento
- Expressão: P’ = S . P

- Rotação
A rotação é o ato de girar o objeto dentro do seu próprio eixo central, fazendo com que ela mude de posição sem mudar o seu ponto central ou seu tamanho. A figura abaixo mostra um exemplo de rotação e a expressão utilizada para cálculo.
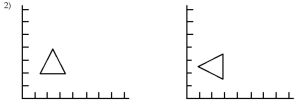
Figura 3.2 – Exercício 2 – Rotação
- Nome da Transformação: Rotação
- Expressão: P’ = R . P
![]()
- Translação
O movimento de translação é quando um objeto troca a posição de todos seus pontos proporcionalmente, fazendo com que ele não altere sua forma dentro do plano cartesiano, segue abaixo a figura exemplificando e a expressão utilizada.
 Figura 3.3 – Exercício 3 – Translação
Figura 3.3 – Exercício 3 – Translação
- Nome da Transformação: Translação
- Expressão: P’ = P + T

- Projeções Geométricas
As Projeções Geométricas permitem a visualização bidimensional de objetos tridimensionais, para isso, é feita a conversão das coordenadas do objeto 2D para o objeto 3D, que resulta na visão do objeto de uma posição específica.
Para a representação do objeto 3D em um plano bidimensional, há a necessidade de três elementos básicos: plano de projeção, raio projetante, e centro de projeção.
O plano de projeção é referente à superfície que será projetado o objeto na forma bidimensional. Os raios de projeção são as retas que passam pelos pontos do objeto e pelo centro da projeção. O centro da projeção é um ponto fixode onde partem os raios de projeção.
- Projeções Paralelas Oblíquas
São projeções que fornecem a sensação espacial e permitem medidas. A direção de projeção não forma 90° com o plano de projeção, mas o plano de projeção é paralelo a um dos três eixos, o que faz com que projeções de faces paralelas a este plano preservam ângulos e distância.
 Figura 4.1 – Projeção Oblíqua
Figura 4.1 – Projeção Oblíqua
- Projeções Paralelas Ortográficas
Na Projeção Paralela Ortográfica, ao contrário da projeção paralela oblíqua, as projetantes são normais ao plano de projeção. Os tipos mais comuns são: vista frontal, superior e lateral. São muito utilizadas em desenhos de engenharia para que possa representar partes de prédios ou máquinas devido as distâncias e os ângulos poderem ser medidos a partir dela.
 Figura 4.2 – Projeção Paralela Ortográfica
Figura 4.2 – Projeção Paralela Ortográfica
- Perspectiva
O conceito de Perspectiva mostra que o centro de projeção é um ponto no espaço, a ser definido, e o objeto é deformado de forma inversamente proporcional à distancia ao centro de projeção. Este tipo de projeção não preserva retas paralelas, com a exceção de que elas estejam em um plano paralelo ao plano de projeção. Em todo caso ela converge para um ponto de fuga, que pode ser qualquer ponto no plano.
 Figura 4.3 – Perspectiva
Figura 4.3 – Perspectiva
- Formas de Representação em um Objeto
- Pivô
O pivô é o marcado pelo centro do objeto, representado pelo ponto (0,0,0) dentro do plano tridimensional. Todos os objetos têm um pivô e um sistema de referência próprio, como mostra a imagem abaixo.

Figura 1 – Ponto Pivô e Sistema de Referência
O ponto pivô é indicado pela cruz no centro do objeto, e as setas indicam o sistema de referência para seus respectivos eixos: vermelho (eixo x), verde (eixo y) e azul (eixo z). O ponto pivô é criado juntamente com o objeto, e é colocado automaticamente em seu centro.
- Wire frame
Neste tipo de representação o software usa apenas as arestas do objeto em uma amostragem 2D, causando uma impressão ambígua do objeto original.
 Figura 2 – Representação por Wire frame
Figura 2 – Representação por Wire frame
Uma vantagem desta representação é a facilidade do sistema utilizar o objeto, pois utiliza apenas arestas.
- Faces
É uma representação de sólidos que usa superfícies limites para descrever seus contornos. Equivale a junção de no mínimo três vértices e por conseqüência três arestas que quando fechadas formam uma face, como mostra a figura abaixo.
 Figura 3 – Representação de Face
Figura 3 – Representação de Face
É uma das formas mais encontradas em modelagem 3D, por ser usada para contornar os objetos modelados.
- Arestas
O conceito de aresta é representado por pelo menos dois vértices que ligadas formam uma linha que é chamada de aresta. A aresta também é utilizada no conceito de wire frame onde o objeto é todo mostrado com arestas.
 Figura 4 – Aresta
Figura 4 – Aresta
- Vértices
Vértices são pontos cuja representação é a menor forma da modelagem. São responsáveis pela criação de qualquer outro objeto.
 Figura 5 – Vértices dispostos aleatoriamente
Figura 5 – Vértices dispostos aleatoriamente
- Técnica de Modelagem
De acordo com a atividade proposta pelo ATPS da matéria de Computação Gráfica, foi requisitado a resposta referente a melhor maneira de se modelar a taça disposta na figura 6.
 Figura 6 – Taça 3D
Figura 6 – Taça 3D
Devido a grande quantidade de detalhes e ao formato da taça é mais viável o uso da técnica de varredura rotacional, que consiste na disposição de vértices ligados, formando uma silueta 2D da taça. Em seguida usa-se o comando “Spin” que rotaciona os vértices com um movimento circular.
